DOE

CASE STUDY

What could be simpler than making microwave popcorn? Unfortunately, as everyone who has ever made popcorn knows, it’s nearly impossible to get every kernel of corn to pop. Often a considerable number of inedible “bullets” (un-popped kernels) remain at the bottom of the bag. What causes this loss of popcorn yield? In this case study, three factors were identified:

1. Diameter of bowls to contain the corn, 10 cm and 15 cm

2. Microwaving time, 4 minutes and 6 minutes

3. Power setting of microwave, 75% and 100%

8 runs were performed with 100 grams of corn used in every experiments and the measured variable is the amount of “bullets” formed in grams and data collected are shown below:

Factor A= diameter

Factor B= microwaving time

Factor C= power

Run order	A	B	C	Bullets (grams)
1	+	–	–	3.28
2	-	+	–	2.28
3	–	-	+	0.74
4	+	+	-	1.28
5	+	–	+	0.95
6	+	+	+	0.32
7	–	+	+	0.28
8	–	-	-	3.12

Full Factorial 

This is the data input

Calculation of the most significant factor. The most significant factor will have the Total Effect (Difference between high and low factor) furthest from 0, be it positive or negative. For this case, the most significant factor is Factor C (Power).

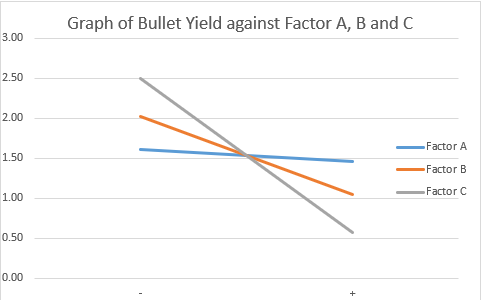
We can also make our life easier by plotting a graph which helps us see more clearly.

From this graph, we can also conclude Factor C (Power) is the most significant factor as it have the steepest gradient. We can also conclude that when the factor is at a higher value, there will be a lesser amount of bullet yield. This can be seen from the decreasing gradient

On a side note, we can also see that the least significant factor is Factor A (Diameter), in fact, it is so insignificant, it make me feel as my life have some significance in comparison. Lastly, Factor B (Microwaving time) is the middle child that is nobody cares about.

Now we can conclude that Factor C (Power) is the most significant factor. Next we shall figure out whether there is interaction between the Factors.

Lets start with Factor A (Diameter) and Factor B (Microwaving time)

If the graph have an intersection, there is interaction, if the graph is parallel, it have no interaction, and if the graph is like the one we see here, there is little to no interaction, hence, we say the interaction is negligible. Therefore, there is no interaction between Factor A (Diameter) and Factor B (Microwaving time)

Next up, Lets look at Factor A (Diameter) and Factor C (Power)

If we look at this graph, The 2 line is going the take eons before they intersect, therefore, we can conclude that the interaction is negligible like the previous case. Hence, There is no interaction between Factor A (Diameter) and Factor C (Power)

Lastly, Lets look at Factor B (Microwaving time) and Factor C (Power)

Once again, the 2 line does not have any intersection, and although they seem like they are moving closer, it is still too insignificant to conclude that there is an interaction. Yet again, we must conclude that the interaction is negligible. Therefore, there is no interaction between B and C

Fractional Factorial

This is the data input

This is the calculation of the significance of the factors. As we can see, the most significant factor is Factor C (Power), just like using the full factorial method. However, there is some difference, such as Factor A (Diameter) instead of reducing the yield of bullet seen in Full factorial, now increases the yield of bullet.

From this graph, we can also conclude Factor C (Power) is the most significant factor as it have the steepest gradient. We can also conclude that when the factor is at a higher value, there will be a lesser amount of bullet yield. This can be seen from the decreasing gradient

In this graph, we can see that Factor B (Microwaving time) also reduces the amount of bullet yield as it increases, just like in the Full Factorial

Now we can conclude that Factor C (Power) is the most significant factor. Next we shall figure out whether there is interaction between the Factors.

Lets start with Factor A (Diameter) and Factor B (Microwaving time)

Just like with the Full Factorial method, there is no, intersection, hence there is no Interaction between 

Factor A (Diameter) and Factor B (Microwaving time).

Next up, Lets look at Factor A (Diameter) and Factor C (Power)

No intersection yet again. Therefore, we can conclude that there is no Interaction between Factor A (Diameter) and Factor C (Power)

Lastly, Lets look at Factor B (Microwaving time) and Factor C (Power)

Once again, There is no intersection. Thus, we can make the same conclusion for the 6th time. There is no Interaction between Factor B (Microwaving time) and Factor C (Power)

So, from this, what can we learn? 

THATS RIGHT!!!  There is no major difference between Full Factorial and Fractional Factorial method, as the trend is the same. Most Significant Factor is the same. Interactions remain the same. However there will be some small difference, as we can see in Factor A (Diameter)

So, why do we need to know that?

THATS RIGHT AGAIN!!! YOU MUST BE A GENIUS.

Knowing this, we can use Fractional Factorial Method instead of Full Factorial Method if we lack resource or time, since the most important part of the data, the most significant factor, will not be affected, 

Here is the link to my Excel Sheet: Case Study.xlsx

Reflection

Design of Experiment is a fun topic to me as we get to analyse data collected and recently I realised that I like to look at Data. However, I am still quite confused on how you should carry out your run order. Other than that part, all is good.